La gravité quantique à boucles — Science étonnante #33

Comment unifier la relativité générale et la mécanique quantique, et percer les mystères des premiers instants du big-bang ? Il n’y a pas que la théorie des cordes ! Le billet qui accompagne la vidéo : https://sciencetonnante.wordpress.com… Me soutenir sur Tipeee : http://www.tipeee.com/science-etonnante Mon livre : http://science-etonnante.com/livre.html Facebook : http://www.facebook.com/sciencetonnante Twitter : http://www.twitter.com/dlouapre Abonnez-vous : https://www.youtube.com/scienceetonnante Crédits de l’animation « géométrie quantique » : T. Thiemann (FAU Erlangen), Max Planck Institute for Gravitational Physics (Albert Einstein Institute), Milde Marketing Science Communication, exozet effects

La gravité quantique à boucles

Comme toujours, quelques commentaires et compléments, un peu plus nombreux que d’habitude. Toutes les parties qui suivent sont indépendantes les unes des autres, n’hésitez pas à passer ce qui ne vous intéresse pas (ou vous semble cryptique).

Gravité quantique et théorie du tout

Un petit point de vocabulaire pour commencer : je parle de théorie du tout et de gravité quantique comme étant la même chose, ça n’est pas tout à fait vrai. La gravité quantique, c’est trouver une théorie quantique de l’interaction gravitationnelle. La théorie du tout, c’est arriver en plus à prendre en compte en même temps toutes les autres interactions. Ca n’est pas la même chose, la théorie du tout est un truc « plus fort », même si quantifier la gravité est très clairement l’obstacle essentiel pour arriver à faire une théorie du tout.

Mais un point important à noter, c’est qu’à ce stade la gravité quantique à boucle n’est qu’une théorie de gravité quantique, alors que la théorie des cordes prétend bien unifier toutes les interactions.

Les manifestations de la relativité générale

Je dis dans la première partie que les effets de la relativité générale se voient surtout dans les champs forts, et je prends comme exemple le cas de Mercure. Certains auront pu tiquer, car si l’on regarde le champ gravitationnel que Mercure ressent du fait du Soleil, il est bien inférieur à celui que l’on ressent à la surface de la Terre (du fait de la Terre). Pour voir les effets de relativité générale, il n’y a pas que l’intensité du champ qui compte, mais aussi le temps d’observation.

Or les déviations (légères) de l’orbite de Mercure (ce qu’on appelle la précession de son périhélie) résultent de l’intégration des effets relativistes sur des périodes longues (une orbite de Mercure prend 3 mois). On peut aussi voir des effets de relativité générale dans le champ gravitationnel terrestre, mais il faut du temps et une grande précision. Le record est une différence mesurée d’écoulement du temps pour deux horloges séparées d’une altitude d’un mètre.

C. W. Chou, D. B. Hume, T. Rosenband, D. J. Wineland (24 September 2010), “Optical clocks and relativity”, Science, 329(5999): 1630–1633

Les équations de la cosmologie

Une fois de plus je parle du Big Bang et de l’évolution du facteur d’échelle. J’en profite pour faire un petit rappel pour les curieux : la cosmologie est une des applications les plus simple de la théorie de la relativité générale ! Si vous savez ce que c’est qu’une équation différentielle ordinaire, vous pouvez tout comprendre.

Je vous renvoie à une série de 3 billets que j’ai écrits sur le sujet :

• Cosmologie 1 : Le Big Bang
• Cosmologie 2 : Forme et destin de l’univers
• Cosmologie 3 : La constante cosmologique

L’instabilité de l’atome de Rutherford

Pour justifier la nécessité de prendre en compte les effets de la mécanique quantique, il y a un exemple dont je parle, que j’aime beaucoup et qui n’est pas forcément très connu : l’instabilité de l’atome de Rutherford.

L’atome de Rutherford, c’est tout simplement le modèle planétaire de l’atome, proposé par le physicien néo-zélandais (le saviez-vous ?) Ernest Rutherford en 1911. On sait que ce modèle a été remplacé par le modèle de Bohr afin de pouvoir expliquer les raies d’émission de l’atome d’hydrogène (ce qui fut un des premiers surgissement de l’idée de quanta dans la physique atomique). Mais sans même de considérations expérimentales, le modèle de Rutherford portait déjà en lui une contradiction : l’atome de Rutherford est instable.

En effet un électron tournant autour d’un proton ferait comme toute particule chargée accélérée : il émettrait un rayonnement électromagnétique. Le système perdrait inexorablement de l’énergie, conduisant à une réduction progressive de l’orbite de l’électron, jusqu’à s’écraser sur le proton. On peut estimer le temps que ça prendrait : environ 10^–11 secondes ! Ce serait donc le temps de vie d’un atome classique.

Classical Lifetime of a Bohr Atom James D. Olsen and Kirk T. McDonald

Les mathématiques de la relativité générale et de la mécanique quantique

Je fais une allusion à la différence de formalisme mathématique utilisé dans les deux théories qui nous intéressent. En relativité générale, on utilise principalement les outils de la géométrie différentielle, et plus précisément de la géométrie Riemanienne. Tout y est continu, lisse, déterministe.

En mécanique quantique (au sens large), on utilise plutôt des outils de l’algèbre linéaire et de la théorie des groupes : espaces de Hilbert, opérateurs, représentations de groupes, etc.

Quand on essaye d’appliquer les concepts de théorie quantique à la relativité générale, on se retrouve naturellement dans des domaines assez velus des mathématiques notamment la topologie algébrique, qui est l’utilisation d’outils algébriques pour étudier des structures topologiques. Petit truc amusant au passage, l’étude de certaines théories de gravité quantique a permis de construire des invariants de variétés, ce qui est une question de mathématiques « pures ». C’est à ma connaissance un des rares cas où les physiciens (et la physique) ont aidé les mathématiciens à résoudre un problème (en général, c’est toujours l’inverse !). Ce sont d’ailleurs ces questions qui ont valu en 1990 la médaille Fields à Edward Witten (le pape de théorie des cordes).

La force électrofaible

Petite remarque pour corriger une petite approximation que j’ai choisi de faire : je dis que la théorie électrofaible est la version « quantique » de la force faible. Ca n’est pas vraiment le cas, puisque la théorie électrofaible correspond à l’unification de l’électrodynamique quantique et de la force faible quantique. On parle rarement de quantifier la force faible « seule ». J’ai vu passer le terme de « Flavodynamique quantique » (QFD) mais il me semble trop marginal pour être utilisé.

La méthode de Dirac

Je raconte sans l’expliquer qu’il existe une méthode pour fabriquer une théorie quantique à partir de sa version classique. C’est ce qu’on appelle la quantification canonique de Dirac. Je voudrais vous donner une saveur de ce à quoi ça ressemble, surtout pour vous montrer à quelle point cette méthode est plus un guide qu’une recette pas à pas, et qu’elle laisse énormément de travail à celui qui espère l’utiliser.

Tout d’abord, il faut partir d’une formulation de la théorie classique sous forme « symplectique » : trouvez les variables de l’espace des phases (par exemple x et p), et le crochet de Poisson associé de sorte que :

et que les équations du mouvement soient sous la forme

où est le hamiltonien et n’importe quelle fonction sur l’espace des phases. Une fois que vous avez ça, vous avez juste reformulé la théorie classique. Et là les difficultés commencent.

Pour faire la théorie quantique, commencez par trouver un espace de Hilbert qui soit en gros l’espace des fonctions de carré sommable des variables de l’espace des phases (en fait de la moitié « x » des variables de l’espace des phases). Quand x est juste un réel, c’est facile. Quand x est une métrique sur une variété riemannienne, on doit essayer de construire un objet horrible qui est l’espace des fonctions de carré sommable sur ces métriques. Bref, un truc mathématiquement hyper pas bien défini.

Imaginons, que vous y arriviez quand même. Deuxième étape, il faut trouver des opérateurs sur cet espace de Hilbert qui vont représenter les variables de l’espace des phases, et qui vont mimer la relation de crochet de Poisson par la relation de commutateur. En gros on cherche des opérateurs X et P tels que

C’est pour ça qu’on résume souvent le programme de quantification de Dirac par l’idée de représenter la relation de crochet de Poisson par le commutateur.

Si on y arrive, il reste encore un certain nombre de difficultés à résoudre pour s’assurer que les symétries sont respectées, que le hamiltonien est bien défini, etc.

Dans le cas précis de la gravité quantique à boucles, une partie des difficultés mathématiques ont été levées, et la construction a été mise sur des bases mathématiques solides, notamment par Thomas Thiemann. Pour les matheux les plus courageux, vous pouvez aller lire

Thiemann, T. (2007). Modern canonical quantum general relativity. Cambridge University Press.

La non-renormalisabilité de la relativité générale

J’ai dit dans la vidéo que si l’on essaye d’appliquer les principes de la quantification perturbative à la relativité générale, on trouve des infinis partout. C’est un gros raccourci de langage.

En fait en général quand on fait de la théorie quantique des champs, on trouve des infinis : c’est ce qu’il se passe par exemple avec l’électrodynamique quantique. Pour guérir les théories de ces infinis, on utilise une méthode appelée « renormalisation », de retrouver le sens physique des expressions infinies. Mais toutes les théories ne sont pas « renormalisables »…et c’est le cas de la relativité générale.

La renormalisabilité d’une théorie peut s’évaluer assez rapidement à partir de ses équations (et de ce qu’on appelle le comptage des puissances). Dans le cas de la relativité générale, grâce à ce comptage on savait depuis longtemps que la renormalisation ne marcherait pas. Mais il fallut attendre les années 80 (et la publication de Goroff et Sagnotti que je montre dans la vidéo) pour que l’on ait une preuve formelle du fait que les infinis ne disparaissaient pas.

Les reformulations de la relativité générale

Je l’ai dit, une des choses qui a débloqué le programme de Dirac pour la relativité générale (et qui a été l’acte de naissance de la gravité quantique à boucles) a été une reformulation de la relativité générale par Abhay Ashtekar. Il existe de nombreuses reformulations de ce genre; la première est due à l’italien A. Palatini, et elle est très ancienne puisqu’elle date de 1919, quelques années après la publication de la théorie de la relativité générale. Je vous cite la publication en italien pour le plaisir :

A. Palatini (1919) Deduzione invariantiva delle equazioni gravitazionali dal principio di Hamilton, Rend. Circ. Mat. Palermo 43, 203–212

Il existe aujourd’hui de nombreuses reformulations qui ont permis de débloquer un aspect ou un autre de la gravité quantique. Comme je l’ai dit, la reformulation d’Ashtekar utilise un formalisme qui ressemble un peu à l’électromagnétisme, ou pour être plus précis, à une théorie de jauge. Si vous regardez l’équation que j’ai mise pour l’action dans les variables d’Ashtekar, on y retrouve E qui est l’analogue d’un champ électrique, et A l’analogue d’un potentiel vecteur (même si c’est plus compliqué que ça.)

Courbure et transport parallèle

J’ai vraiment hésité à présenter cela dans la vidéo, mais je ne pouvais décemment pas parler de gravité quantique à boucles sans expliquer d’où venait le terme de « boucle ». Ces boucles sont ce qu’on appelle parfois les boucles de Wilson, et sont classiques dans le domaine des théories de jauge. Comme je l’explique dans la vidéo, ces notions permettent de capturer l’idée de courbure.

Je suis sur que mon exemple de transport de vecteur sur la sphère va interpeller plein de gens, et pourtant c’est bien de cela qu’il s’agit. C’est la notion dite de transport parallèle. Quand le transport parallèle le long d’une boucle dépend du chemin suivi, c’est que l’on est en présence de courbure, et c’est cela que capturent les boucles de Wilson. On peut donc utiliser les boucles comme variables de la théorie, plutôt que d’utiliser la métrique.

Les réseaux de spin

J’ai illustré le fait qu’en gravité quantique à boucles, un état quantique de l’espace est représenté par un réseau, appelé réseau de spin. J’ai passé sous silence un point important qui explique ce nom : sur chaque arête du réseau on met un nombre demi-entier. C’est à dire que pour décrire complètement un état quantique, on doit donner un graphe et spécifier un demi-entier sur chaque arête. On peut prendre l’analogie avec l’atome d’hydrogène : un état propre de l’atome d’hydrogène est décrit par trois nombres quantiques n,l et m. Un état propre de la gravité quantique à boucle est décrit par un graphe muni d’un nombre quantique sur chaque arête. On parle donc de réseau « de spin » à cause de ces nombres demi-entiers (il n’y a pas de notion de moment cinétique, donc).

Ces nombres ont un sens physique : il correspondent à la quantification de l’opérateur d’aire.

D’ailleurs j’ai entretenu une confusion savante entre le réseau de spin et la vision « discrète » de l’espace. Le réseau de spin n’est pas l’espace « triangulé », mais presque. Pour rétablir la vérité : les briques d’espace sont le « dual » du réseau de spin. A chaque noeud du graphe correspond un volume, à chaque arête correspond une aire (d’où l’idée que les arêtes du réseau portent les nombres quantique de l’opérateur d’aire).

La cosmologie quantique à boucles

Quelques précisions sur ce qu’est réellement la cosmologie quantique à boucle (du moins à l’heure actuelle).

La cosmologie classique, c’est la relativité générale réduite au cas très particulier (et simple) d’un Univers homogène et isotrope. Si on voulait vraiment faire de la cosmologie quantique, il faudrait partir de la relativité générale, la quantifier pour obtenir une théorie de gravité quantique « complète », puis réduire cette théorie au cas d’un univers homogène isotrope. Ca n’est pas ce que fait la « Loop Quantum Cosmology » ! Elle fait essentiellement l’inverse : elle applique les principes de la gravité quantique à boucle à la cosmologie classique : en gros on réduit puis on quantifie, au lieu de quantifier puis réduire. Vous voyez la différence ?

Cela permet de beaucoup simplifier les calculs, car on quantifie une théorie relativement simple (la cosmologie classique). Mais a priori on n’est pas assuré que la quantification du modèle réduit correspond bien à la réduction du modèle quantifié !

Cosmologie quantique et fluctuations du CMB

Les derniers travaux que j’évoque sont tous récents, et j’avoue que je ne les connaissais pas avant de préparer cette vidéo ! Comme je l’explique, la source la plus riche que l’on ait sur le Big Bang, ce sont les fluctuations du rayonnement fossile. J’avais déjà parlé de ces fluctuations dans un billet (le rayonnement fossile et ce que Planck nous en révèle). Un point essentiel est que le spectre de puissance des fluctuations angulaires nous permet de tester tout un tas d’hypothèses sur ce qu’il s’est passé dans les premiers instants du Big Bang. C’est par exemple par ce moyen que la collaboration BICEP2 croyait avoir « prouvé » l’inflation par la découverte des ondes gravitationnelles primordiales (voir « Ondes gravitationnelles ? Inflation ? Ou les deux ?« ). On a su par la suite que c’était une erreur, mais l’idée est là.

C’est ce qu’on aussi utilisé Abhay Ashtekar et Aurélien Barrau pour calculer ce que pourrait être une signature de la cosmologie quantique à boucle.

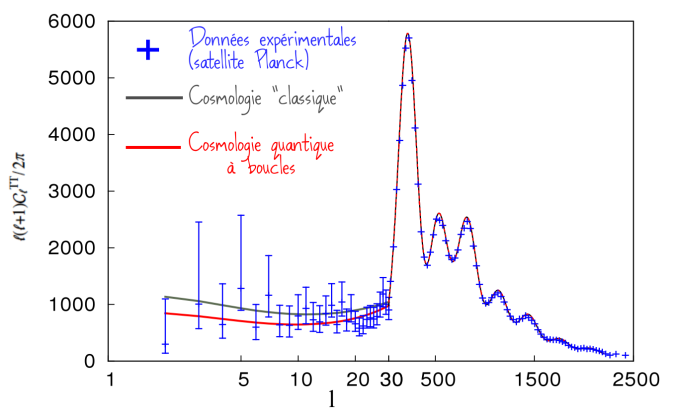Dans ce graphique que j’ai adapté de leur publication, on voit le spectre de puissance des fluctuations tel que donné par les valeurs expérimentales (bleu), la cosmologie classique (gris) et la cosmologie quantique à boucle (rouge). On voit que ces deux dernières diffèrent aux faibles « l », c’est à dire pour les fluctuations sur de grandes tailles angulaires. Il se trouve que ces fluctuations sont les plus difficiles à mesurer, donc dans cette zone les barres d’erreur sont énormes et on ne sait pas encore discriminer entre les deux modèles. Mais il est envisageable que ce soit le cas un jour. On pourrait alors tester expérimentalement la cosmologie quantique à boucles ! Comme je le dis en conclusion, c’est très important car cette théorie devient « réfutable », contrairement à d’autres approches de gravité quantique (suivez mon regard) qui ont tellement de paramètres libres qu’elles s’accommoderaient de n’importe quel résultat expérimental…ce qui poussent certain à dire que la théorie des cordes ne fait pas partie de la science !

Rayons cosmiques et structure quantique de l’espace temps.

Sur la possibilité de sonder la structure quantique de l’espace temps par des rayons cosmiques de haute énergie, je vous renvoie à ce billet que j’avais écrit il y a longtemps :

Des rayons cosmiques très énergétiques…trop énergétiques ?

Quand j’étais étudiant en thèse, il y avait une approche très populaire qui était apparue qui consistait à essayer de modifier la relativité restreinte (je dis bien « restreinte ») pour prendre en compte des effets de structure discrète de l’espace temps. En gros l’idée était que l’on pouvait chercher une relativité « double » dans laquelle à la fois la vitesse de la lumière et la longueur de Planck seraient des invariants. Ce type d’approche présentait justement des conséquences sur la manière dont certains rayons très énergétiques pouvaient se propager.

Voir « Doubly special relativity« 

J’imagine que seuls quelques personnes sont arrivées jusqu’à la fin de cet article : félicitations à vous 🙂

(120)